[ad_1]
Whenever a data scientist works to predict or classify a problem, he first detects accuracy using the model trained for the train set, and then for the test set. If the precision is satisfactory, i.e. the precision of training and testing is good, then a particular model is considered for further development. But sometimes the models give bad results. A good machine learning model aims to generalize training data well to all data in that domain. So why is this happening? Here is the main cause of the poor performance of machine learning models is Overfitting and Insufficiency. Here we explain in detail what is overfitting and underfitting and achieving the effect via Python coding and finally, some techniques to overcome these effects.
The terms overfitting and underfitting tell us whether a model is successful in generalizing and learning new data from invisible data to the model.
Register for this Free Session>>
Brief information on overfitting and underfishing
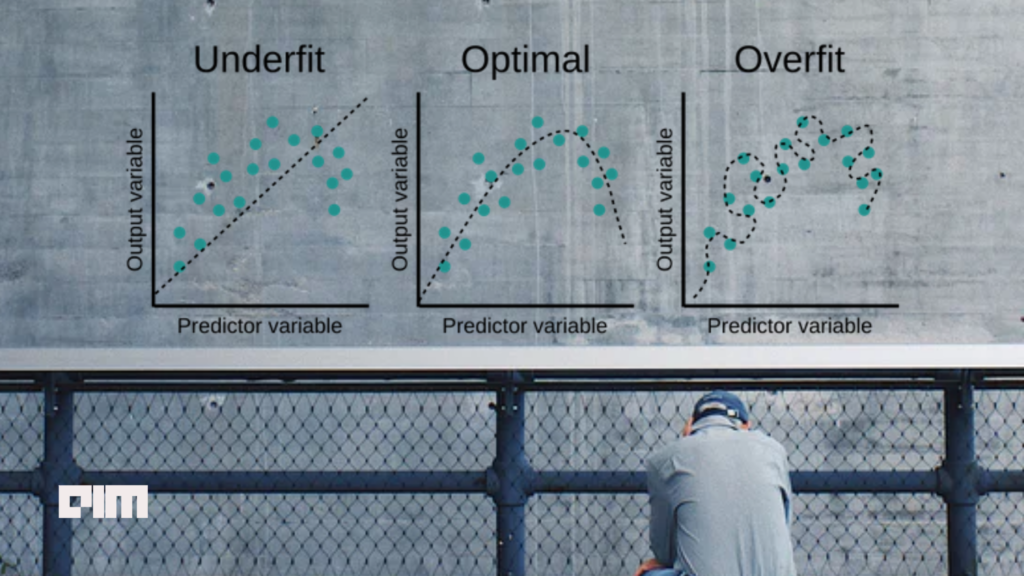
Clearly understand overfitting, underfitting, and perfectly fitting models.
From the three graphs shown above, it can be clearly understood that the line in the leftmost figure does not cover all data points, so we can say that the model is underfit. In this case, the model failed to generalize the model to the new dataset, which resulted in poor performance during testing. The under-fitted model can be easily seen as it gives very high errors on training and test data. This is because the data set is not clean and contains noise, the model has a high bias and the size of the training data is not sufficient.
Regarding overfitting, as the right-most graph shows, it shows that the model is covering all data points correctly, and you might think it’s a perfect fit. But actually, no, it’s not a good fit! Since the model learns too much detail from the dataset, it also takes noise into account. Thus, this negatively affects the new data set; not all of the details that the model learned during training needs also apply to the new data points, resulting in poor performance on tests or the validation dataset. Indeed, the model was trained in a very complex way and has a high variance.
The best fit model is shown by the middle graph, where the loss of training and testing (validation) is minimal, or we can say that the accuracy of training and testing should be close to each other and have a high value.
Practical observation of the effect of over-learning and under-learning:
We will check the correctness and error of two regression models, namely the Decision Tree regressor and the linear regression.
The diabetes data set integrated with Sklearn is used for the modeling.
Import the necessary libraries.
import matplotlib.pyplot as plt  import pandas as pd import numpy as np from sklearn.datasets import load_diabetes from sklearn.metrics import mean_absolute_error from sklearn.model_selection import KFold from sklearn.linear_model import LinearRegression from sklearn.tree import DecisionTreeRegressor
Loading the dataset and selecting the input and output entities. It is not necessary to preprocess the data because it is already preprocessed.
load_data = load_diabetes() # Load the dataset x = load_data.data   # selecting input features y = load_data.target  # target variable pd.DataFrame(x,columns=load_data.feature_names).head() # See the distribution of data
Here’s what the data looks like:
To split the data into training and test tests here, I used K-Fold cross validation, which gives K number of training and test data, which helps to get the accuracy and errors by relative to the number of sub-assemblies.
The approach I have taken is fairly straightforward. Twenty folds are created, which are then used to obtain training and testing accuracy for each fold stored in the list, and the same is done for the mean absolute error. Finally, four graphs are displayed for the train test error and the accuracy of the train test, which clearly shows the insight of this test.
The code used for linear regression and decision tree is completely the same, only the change is the estimation function, i.e. the algorithm is changed where our model is defined. That is why here only the code for linear regression is displayed.
 kf = KFold(n_splits=20,shuffle=True) # defining fold parameter # created empty list to append score and error training_error = [] training_accuracy = [] testing_error = [] testing_accuracy = [] for train_index,test_index in kf.split(x):     # divide the data into train and test     x_train,x_test = x[train_index],x[test_index]     y_train,y_test = y[train_index],y[test_index]     #load the Linear Regression model     model = LinearRegression()     model.fit(x_train,y_train)     #get the prediction for train and test data     train_data_pred = model.predict(x_train)     test_data_pred = model.predict(x_test)     #appending the errors to the list     training_error.append(mean_absolute_error(y_train,train_data_pred))     testing_error.append(mean_absolute_error(y_test,test_data_pred))     #appending the accuracy to the list     training_accuracy.append(model.score(x_train,y_train))     testing_accuracy.append(model.score(x_test,y_test))
Code to display precision and error plots of train and test data.
plt.figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.plot(range(1,kf.get_n_splits()+1),np.array(training_error).ravel(),'o-')
plt.xlabel('No of folds')
plt.ylabel('Error')
plt.title('Training error across folds')
plt.subplot(2,2,2)
plt.plot(range(1,kf.get_n_splits()+1),np.array(testing_error).ravel(),'o-')
plt.xlabel('No of folds')
plt.ylabel('Error')
plt.title('Testing error across folds')
plt.subplot(2,2,3)
plt.plot(range(1,kf.get_n_splits()+1),np.array(training_accuracy).ravel(),'o-')
plt.xlabel('No of folds')
plt.ylabel('Accuracy')
plt.title('Testing accuracy across folds')
plt.subplot(2,2,4)
plt.plot(range(1,kf.get_n_splits()+1),np.array(testing_accuracy).ravel(),'o-')
plt.xlabel('No of folds')
plt.ylabel('Accuracy')
plt.title('Testing accuracy across folds')
Linear regression plot output:
Decision tree output plot:
Conclusion:
If we compare the two algorithms for linear regression, this is clearly stated in the 1st and 2nd plots, the training and testing error is almost the same, but it is significantly high, and for the precision shown in the 3rd and 4th plots, the accuracy of the train and the test is almost the same, but again it is considerably low. So from the above explanation, can you guess what’s wrong with this model? If you guessed the underfit then yes you are right it is an underfit issue. The linear regression model fails to learn the models associated with the training dataset, nor does it fail to generalize it to the test set.
From the decision tree plot, if you see the 1st and 2nd error plots for training and testing respectively, surprisingly the error is literally zero for the learning set and for the tests it showed a huge amount of errors. The same is observed for the precision plots also where the precision of the formation is 100%, and on the other hand, the accuracy of the tests is greater than –80%. Getting less precision means that for fold number 16, the regression line does not follow the trend of the data and it makes no sense. So you might have guessed that this is an overfitting issue. As explained previously, when forming a decision tree, the algorithm learns too much from the data. That’s why it failed on the test dataset.
here is Colab notebook for the implementation of the above code
End points:
So is there a way to fix these issues? The most common problem encountered is overfitting, and also, it is more important to know if a model is overfit rather than underfit. Because the evaluation on the tests is very different from the actual results that interest us the most. Here you will find various techniques used to deal with overfitting and underfitting issues.
Again, this is a kind of black box, where you have to train and test your model for various algorithms in order to limit these issues.
Join our Discord server. Be part of an engaging online community. Join here.
Subscribe to our newsletter
Receive the latest updates and relevant offers by sharing your email.
[ad_2]